Context
I've been reading the book Grokking Deep Learning by Andrew W. Trask and instead of summarizing concepts, I want to review them by building a simple neural network. This neural network will use the concepts in the first 4 chapters of the book.
What I'm Building
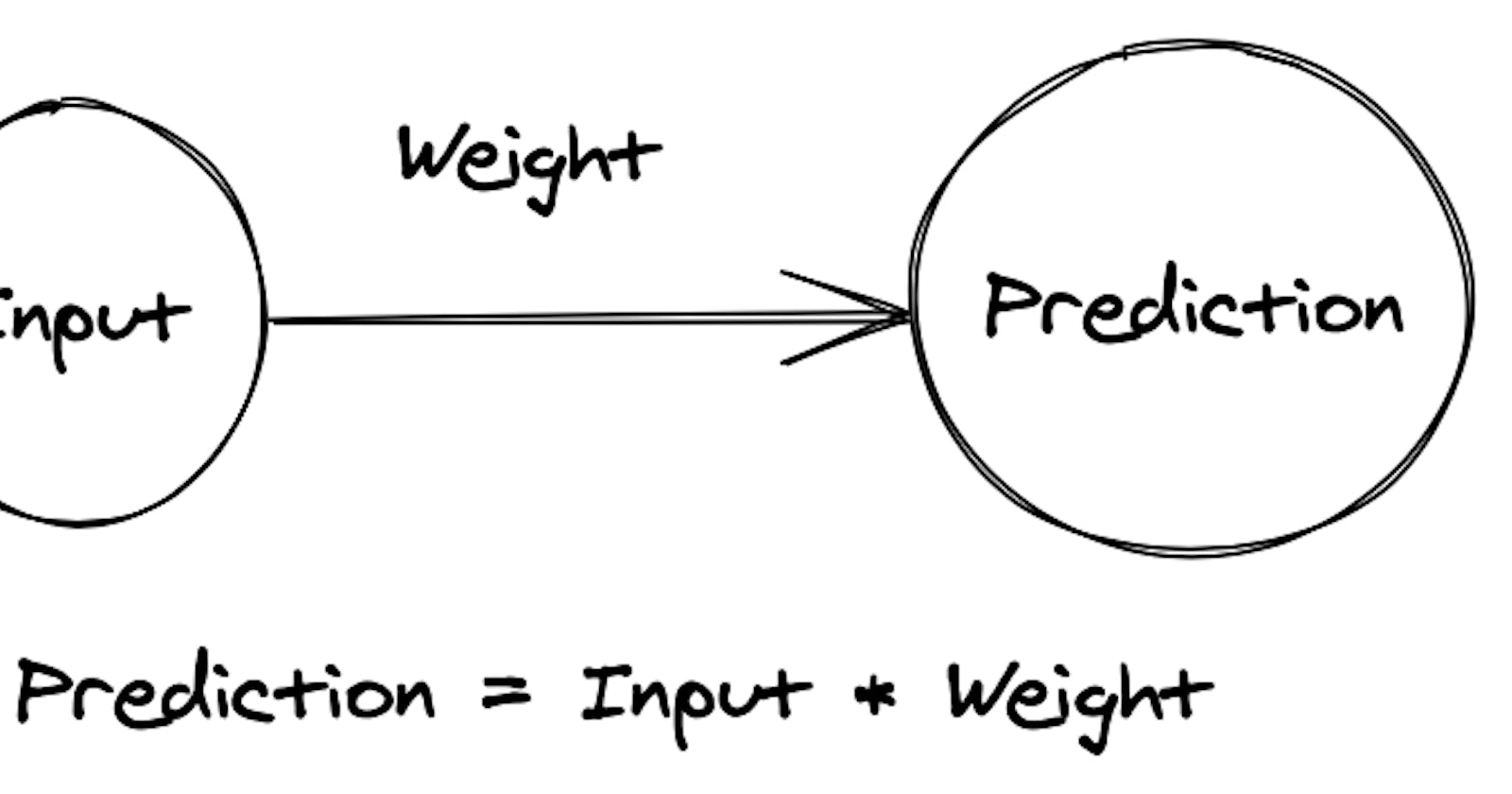
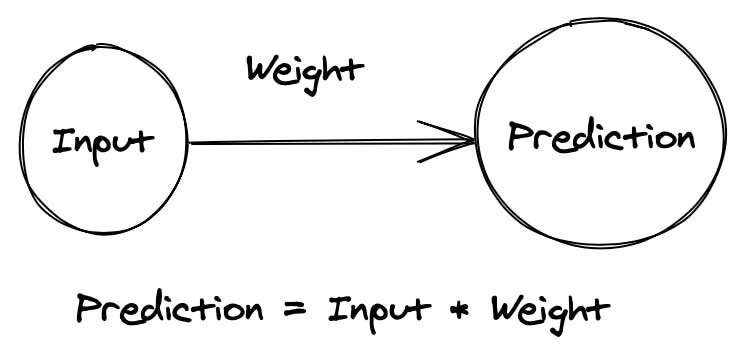
I'm going to build a neural network which outputs a target number given a specific input number. For example, given the number 5, I want the neural network to output the number 42.
Now I can hear you think to yourself, "That's stupid. How is that better than a function with the line return 42 in the body?"
What's cool about this code is that I didn't type the number 5 or 42 anywhere in the body of the network. Instead, I told the network I wanted it to print 42 when it received 5 as an input and it figure out how to adjust itself to do that.
In fact, I could train the network on any 2 numbers using the same code. Try changing the parameters yourself and test it out!
With that context, let's see what the code looks like for this most simple neural network.
The Code
# A simple neural network class
class SimpleNN:
def __init__(self):
self.weight = 1.0
self.alpha = 0.01
def train(self, input, goal, epochs):
for i in range(epochs):
pred = input * self.weight
delta = pred - goal
error = delta ** 2
derivative = delta * input
self.weight = self.weight - (self.alpha * derivative)
print("Error: " + str(error))
def predict(self, input):
return input * self.weight
# Create a new SimpleNN
neural_network = SimpleNN()
# Train the SimpleNN
neural_network.train(input=5, goal=42, epochs=20)
Error: 1369.0 Error: 770.0625 Error: 433.16015625 Error: 243.6525878906251 Error: 137.05458068847665 Error: 77.09320163726807 Error: 43.36492592096329 Error: 24.39277083054185 Error: 13.72093359217979 Error: 7.718025145601132 Error: 4.341389144400637 Error: 2.442031393725358 Error: 1.373642658970514 Error: 0.7726739956709141 Error: 0.43462912256489855 Error: 0.24447888144275018 Error: 0.13751937081154697 Error: 0.07735464608149517 Error: 0.043511988420844 Error: 0.02447549348672308
neural_network.predict(5)
41.88266515825944
After 20 rounds of training, the network's final prediction is off by about 0.02. Not bad!
Even in this barebones neural network, there's a lot going on. Let's take it line by line.
Neural Networks
A neural network is a collection of weights being used to compute an error function. That's it.
The interesting thing about this statement is that for any error function, no matter how complicated, you can compute the relationship between a weight and the final error of the network. Therefore, after each prediction, we can change each weight in the network to inch the final error towards 0.
Let's take a look what a neural network needs to make a prediction.
The 2 Things A Neural Network Needs To Make A Prediction
The Weight
self.weight = 1.0
I mentioned before that a neural network is just "a collection of weights". So what are weights?
weight is a number that the neural network stores and remembers. It can be thought of of the "memory" of the network. After each round of training, the network updates the weight to make more accurate predictions.
In our network, I set weight=1.0. I just used trial-and-error to figure out a good starting weight for this problem.
The Input
def train(self, input, goal, epochs):
def predict(self, input):
input is a number that the neural network accepts. This can be thought of as information from the outside world.
In our network, I set input=5 when I start training the network.
So how does this thing learn?
I use a method called Stochasitc Gradient Descent to get SimpleNN to learn the training data.
At a high level, the 4 step process is:
- Make a prediction using a given input
- Calculate the error
- Calculate the derivative to tell us how much to adjust the weights by
- Adjust the weight and go back to step 1.
1. The Prediction
pred = input * self.weight
When the neural network has both an input and weight, it multiplies them together to make a prediction. Every single neural network, from the most simple to ones with 1000s of layers works this way.
2. How much are we off by?
delta = pred - goal
error = delta ** 2
So we've seen that the network make a prediction by multiplying input and weight. After it makes a prediction, the network is able to calculate how much it was off by.
A neural network learning is all about error attribution. How much did each weight contribute to the overall error of the system and how can we change the weight so that error is minimized? In our example, it's easy to figure out since there is only 1 weight.
How do we calculate the error? One thing we need to keep in mind is that we want the error to be a positive number. If the error is allowed to be negative, multiple errors might accidentally cancel each other out when averaged together.
In our case, we square the amount we are off by. Why square instead of something straightforward like absolute value? Squaring gives us a sense of importance. Large errors are magnified while small errors are minimized. Therefore, we can prioritize large errors before small errors. Absolute value doesn't give us this additional sense of importance.
3. Adjusting the weights
derivative = delta * input
self.weight = self.weight - (self.alpha * derivative)
The network figures out how much to adjust the weights by using a derivative. How does derivative play into this process? What a derivative tells us is the direction and amount one variable changes when you change a different variable. In our case, derivatives tell us much much error changes when you change the weight. Given that we want error to be 0, this is exactly what we need.
The network calculates the derivative by multiplying the delta by the weight's input to get the weight_delta. weight_delta is the direction and the amount we're going to change the weight by.
self.alpha = 0.01
One bit of nuance is the variable alpha. alpha is a throttle limiting how much we actually adjust the weights. Determining the appropriate rate of change for the weights of a neural network is a challenge. If the steps are too large, the network will overshoot the error getting to zero and start acting in unpredictable ways. If the steps are too small, the network will take a long time and need a very large number of training cycles.
The solution to this problem is to multiply partial derivative by a single number between 0 and 1. This lets us control the rate of change and adjust the learning as needed.
Finding the appropriate alpha is often done through trial and error so we're just going to hard code is here.
4. Training rounds
neural_network.train(input=5, goal=42, epochs=20)
for i in range(epochs):
Finally, there's the concept of epochs. This refers to the number of times the network will go through the entire data set. The appropriate number of epochs for a problem will often be found through trial and error.
I'm using 20 in the example, which I found by running the training with different epochs and picking the lowest one with an acceptable error. Feel free to experiment with the number of epochs and see what happens at different numbers.
So what did I accomplish?
I'm able to give the neural network the number 5, and have it output a number very close to our goal number 42 without putting the number 5 or 42 in the body of the function.
I also learned the basic parts which make up all neural networks and we learned the process of how the network learns.
As we start to move into networks with multiple inputs, multiple outputs, and multiple layers, it's going to get a lot more complicated. However, the mental model stays the same. The network makes a prediction by multiplying the received input with its stored weights. It measures the error, takes the derivative, and adjusts the weights so that error moves towards 0. Then it goes again.
What's next?
I'm going to tackle multiple inputs and multiple outputs. I'll see how matrices come into play and how we can build a simple library to do matrix math.
See you then!